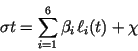Tidal Spherical Harmonics
The convention used here for spherical harmonics of tidal elevations
is similar to that used by
Lambeck (1980, eq. 6.2.1--allowing for a misprint in his 6.2.1c),
except for some changes in phase for diurnal tides.
Like Lambeck, we use strictly phase lags in the tidal arguments.
The usual convention in satellite geodesy is to use phase leads.
Generally, most of the tidal literature uses unnormalized coefficients,
which we also employ here.
For any given harmonic constituent
of frequency 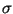 , we express the tidal height fluctuation
, we express the tidal height fluctuation
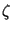 (reckoned relative to the seabed) as
(reckoned relative to the seabed) as
comprising prograde  and retrograde
and retrograde 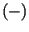 waves of amplitude
waves of amplitude
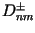 and phase lag
and phase lag 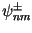 , where
, where 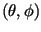 are
spherical polar coordinates and
are
spherical polar coordinates and 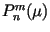 is
an associated Legendre function (unnormalized).
Note that in this context, ``prograde'' means in the direction of
the tide-raising body, i.e., westward;
this usage is standard in tidal literature but is opposite to that
used in polar motion studies.
The
is
an associated Legendre function (unnormalized).
Note that in this context, ``prograde'' means in the direction of
the tide-raising body, i.e., westward;
this usage is standard in tidal literature but is opposite to that
used in polar motion studies.
The 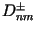 and
and
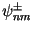 parameters are deduced from numerical hydrodynamic models
or from satellite altimeter measurements
of the global tide; this is done
by direct numerical quadrature over the globe (here assumed spherical)
of the tidal elevations.
Some of the parameters
(mainly those of order 1 for diurnal tides and 2 for semidiurnal)
can be deduced from analysis of satellite orbit perturbations.
parameters are deduced from numerical hydrodynamic models
or from satellite altimeter measurements
of the global tide; this is done
by direct numerical quadrature over the globe (here assumed spherical)
of the tidal elevations.
Some of the parameters
(mainly those of order 1 for diurnal tides and 2 for semidiurnal)
can be deduced from analysis of satellite orbit perturbations.
The variable 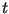 is time reckoned from some conventional point that
is generally different for each tidal constituent. For example,
for M
is time reckoned from some conventional point that
is generally different for each tidal constituent. For example,
for M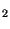 time is reckoned from the instant the mean moon passes the
Greenwich meridian. More clearly, the argument
time is reckoned from the instant the mean moon passes the
Greenwich meridian. More clearly, the argument 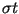 is equal
to a linear combination of the Brown astronomical longitudes:
is equal
to a linear combination of the Brown astronomical longitudes:
where the 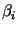 are the Doodson numbers for the given tidal constituent
and
are the Doodson numbers for the given tidal constituent
and 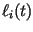 are the astronomical longitudes:
are the astronomical longitudes:
The additional angle 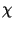 is employed so that we may consistently use
cosine functions above and also maintain positive amplitudes;
this is standard following Doodson's convention.
For the primary tides we have
is employed so that we may consistently use
cosine functions above and also maintain positive amplitudes;
this is standard following Doodson's convention.
For the primary tides we have  for
the semidiurnals M
for
the semidiurnals M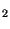 , N
, N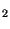 , S
, S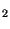 , K
, K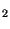 , (but 180
, (but 180 for the small tide
R
for the small tide
R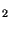 );
);  for the long-period tides Sa, Ssa, Mm, Mf, Mt;
but
for the long-period tides Sa, Ssa, Mm, Mf, Mt;
but 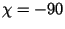
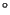 for Q
for Q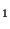 , O
, O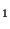 , P
, P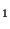 , and
, and 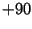
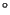 for K
for K .
.
Lambeck, K., The Earth's Variable Rotation,
Cambridge Univ. Press, 1980.
Doodson, A. T. and H. D. Warburg, Admiralty Manual of Tides,
HMSO, 1941.
Richard Ray
2000-03-29
![]() , we express the tidal height fluctuation
, we express the tidal height fluctuation
![]() (reckoned relative to the seabed) as
(reckoned relative to the seabed) as
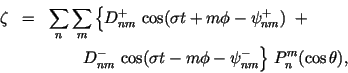
![]() is time reckoned from some conventional point that
is generally different for each tidal constituent. For example,
for M
is time reckoned from some conventional point that
is generally different for each tidal constituent. For example,
for M![]() time is reckoned from the instant the mean moon passes the
Greenwich meridian. More clearly, the argument
time is reckoned from the instant the mean moon passes the
Greenwich meridian. More clearly, the argument ![]() is equal
to a linear combination of the Brown astronomical longitudes:
is equal
to a linear combination of the Brown astronomical longitudes: